讨论班 | ESL讨论班、学术交流研讨班、因果推断讨论班(2021/5/10-2021/5/16)
1、讨论班简介
ESL讨论班
针对新同学开展统计学习精要的学习,主讲机器学习知识。课程内容以《The Elements of Statistical Learning》为主,部分延伸内容需要参考辅助书目;
学术交流研讨班
针对博士生开展,主要形式为学术论文讨论交流。
因果推断讨论班
研究主题包括复杂数据的因果推断,精准治疗/决策,IV, DID, RDD, mediation等计量方法,异质性因果效应,因果机器学习,因果网络发现,非参检验,多源数据融合的因果分析和匹配、加权等经典方法的最新进展。
2、时间及地点
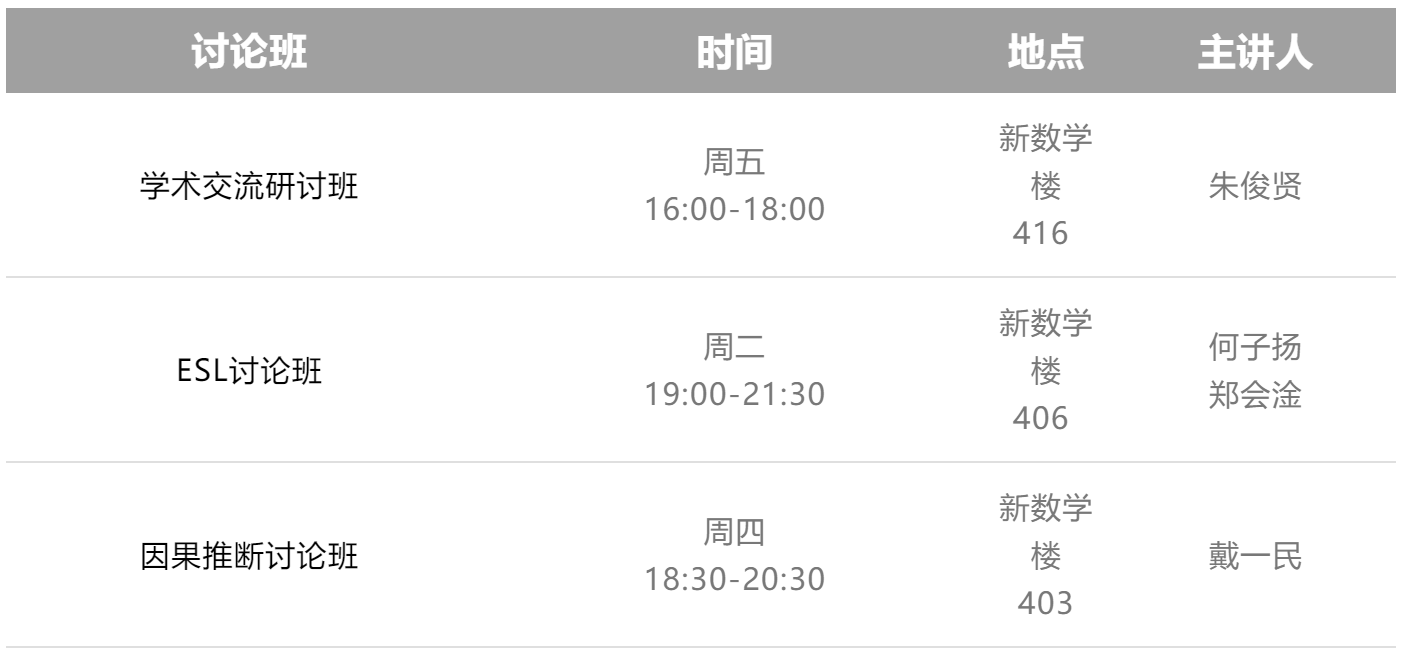
3、本期内容概述
ESL讨论班
支持向量机(Support Vector Machine)是一类稳健地进行分类或回归的线性或非线性学习器,是理论基础较为完善的有监督学习方法之一。本章我们将介绍SVM的基本内容及其推广,其中重点内容为SVM的理论推导以及核方法在其中的应用。此外,我们还将介绍由Fisher线性判别方法(Linear Discriminent Analysis)推广而来的可变判别分析(Flexible Discriminet Analysis)及相关方法。
学术交流研讨班
最优子集选择问题是指在回归模型中用于建模的解释变量尽可能少的同时保持理想的预测准确性。它在包括统计学、计算机科学、经济学和医学在内的众多领域都有着广泛的应用;同时,它的求解是一个经典的NP困难问题。本文针对最优子集选择问题,在线性模型、低信噪比情形以及广义线性模型展开研究,取得如下成果:在第二章中,我们考虑线性回归的最优子集选择问题,提出了剪接技术,一种利用排序和交换达到稳定解的方法。基于该技术,发展了ABESS算法,并证明了该算法估计的激活集会包含真实激活集且给出了该算法的迭代步数以及估计误差的上界。在稀疏性水平未知的情形下,结合信息准则,ABESS算法会复原真实激活集。我们还证明了ABESS算法的计算复杂度是多项式时间的。在第三章中,我们考虑低信噪比情形的最优子集选择问题。我们提出正则化的最优子集选择方法,因为它能更好地平衡偏差和方差。我们还提出一种崭新且高效的算法,并对其进行理论论证与数值实验验证。在第四章中,我们推广最优子集选择问题到广义线性模型,给出了该模型的剪接过程,并提出GABESS算法。结合广义信息准则,我们证明了GABESS算法依概率1恢复真实激活集。最后,数值实验证实了该算法的理论结果。
因果推断讨论班
Inverse probability weighting (IPW) is widely used in empirical work in economics and other disciplines. As Gaussian approximations perform poorly in the presence of “small denominators,” trimming is routinely employed as a regularization strategy. However, ad hoc trimming of the observations renders usual inference procedures invalid for the target estimand, even in large samples. In this article, we first show that the IPW estimator can have different (Gaussian or non-Gaussian) asymptotic distributions, depending on how “close to zero” the probability weights are and on how large the trimming threshold is. As a remedy, we propose an inference procedure that is robust not only to small probability weights entering the IPW estimator but also to a wide range of trimming threshold choices, by adapting to these different asymptotic distributions. This robustness is achieved by employing resampling techniques and by correcting a non-negligible trimming bias. We also propose an easy-to-implement method for choosing the trimming threshold by minimizing an empirical analogue of the asymptotic mean squared error. In addition, we show that our inference procedure remains valid with the use of a data-driven trimming threshold. We illustrate our method by revisiting a dataset from the National Supported Work program. Supplementary materials for this article are available online.


