讨论班 | 函数型数据、网络分析(2021/9/27-2021/10/3)
1、讨论班简介
函数型数据讨论班
本讨论班的研究主题是函数型数据的平滑方法、主成分分析、典型关联分析、线性模型、微分方程与算子等,有助于大家在日常的学习研究当中从函数型数据的角度分析问题,剖析复杂数据下的本质特征,获得更合理、更直观的数据解释。
网络分析讨论班
本讨论班讲授的主要内容是《Social and Economic Network》,旨在让大家对社会网络和经济网络分析有一个全面的认识,为理解和分析网络奠定理论基础。主要研究内容包括随机网络模型、网络结构分析、网络传播与渗透阈值、博弈论等。
2、时间及地点
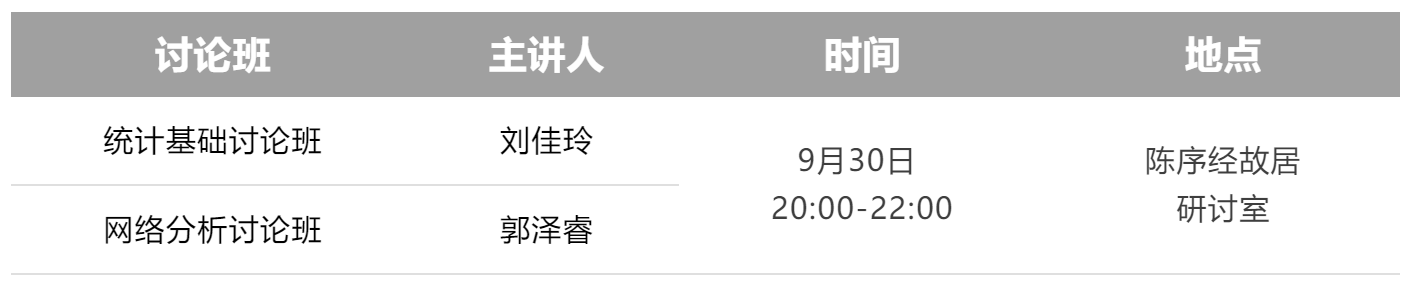
3、本期内容概述
函数型数据讨论班
时间序列
按照时间顺序把随机事件发展变化的过程记录下来就构成了一个时间序列。时间序列分析可以用于描述系统和预测未来。
本节讨论班主要介绍时间序列建模中的ARMA模型,它是一种以自回归模型(AR模型)和移动平均模型(MA模型)为基础“混合”构建而成的线性模型。
网络分析讨论班
Percolation, Component Size, Immunity, and Diffusion
Identifying whether there are pathways linking various nodes in the network is essential to the broader concerns of infection, navigation, and information transmission in society. We realize that individual connection is sporadic, or that it must fulfill specific criteria before it may spread. This leads to the overlap with physical and mathematical literature's "percolation theory", which is comparable to determining if a path exists from one end of the network to the other. As a result, percolation theory's methods and insights are applied to the study of diffusion and navigation on networks, which in turn enriches the theory.


